回复: [无聊]马克思基本原理
原帖由 Prz 于 2008-12-25 12:54:00 发表
"观测"不可能"证明"任何东西。
考数学让你证明三角形内角和等于180度,你不能在考卷上画100个形状不同的三角形,然后说,观测证明了…… |
平移的特征 (1)平移后的图形与原来的图形的对应线段平行且相等,对应角相等,图形的形状和大小都没有发生变化。(2)图形平移后对应点所连的线段平行且相等。
方法一:把三角形的某一边平移到它所对的顶点上。
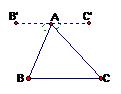
例1:把BC向A点平移到如图所示。
根据平移的特征,可知:B/C/∥BC。
∴∠B/AB=∠B,∠C/AC=∠C。
∵∠B/AB+∠BAC+∠C/AC=180
∴∠BAC+∠B+∠C=180。
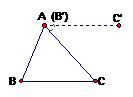
例2:如图,将BC边沿BA方向平移到A点。
则AC/∥BC。
∴∠C/AC=∠C。
∴∠BAC/+∠B=180。
∴∠B+∠C+∠BAC=180。
方法二:把三角形的三条边同时向三角形内平移至某一点P。
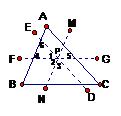
例3:如图,把AB、AC、BC分别平移到△ABC内交于一点P。
∵DE∥AC,MN∥AC,FG∥BC。
∴∠1=∠5=∠C,
∠2=∠4=∠B,
∠3=∠6=∠A。
∵∠1+∠2+∠3=180,
∴∠A+∠B+∠C=180。
方法三:把三角形的两条边沿第三条边相对方向移动端点交于其边上的某一点。
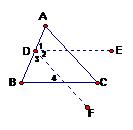
例4:如图,把BC、AC沿AB边相对移到点D,则:
DE∥BC,DF∥AC。
∴∠1=∠B,
∠2=∠4=∠C,
∠3=∠A。
∵∠1+∠2+∠3=180,
∴∠A+∠B+∠C=180。
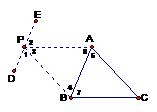
方法四:把三角形的三边分别平移到三角形的外部交于某一点。
例5:如图,把AC沿CB方向平移到B点,BC沿CA方向平移到A点,平移后两线段交于一点P,将AB平移到点P。则:
PA∥BC,PB∥AC,DE∥AB。
∴∠1=∠4=∠7,
∠2=∠6=∠5,
∠3=∠C。
∵∠1+∠3+∠2=180,
∴∠ABC+∠C+∠BAC=180。
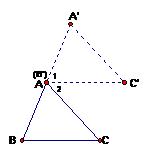
方法五:把三角形整体沿某一边所在的直线平移。
例6:如图,把△ABC沿BA方向移到A。
根据平移的性质特征,可知:
∴∠1=∠B,且AC/∥BC,
∴∠2=∠C。
∵∠1+∠2+∠BAC=180,
∴∠ABC+∠B+∠C=180。

allfox 最后编辑于 2008-12-25 13:07:20