RT。
马上要考final,我也在死磕各科争取漂亮一些的GPA嗯……
刚才,我做了一道题……
答案都正确得出了,不过其中有些东西想不通,请求KeyFC诸位数学/物理/生物帝指导启蒙……
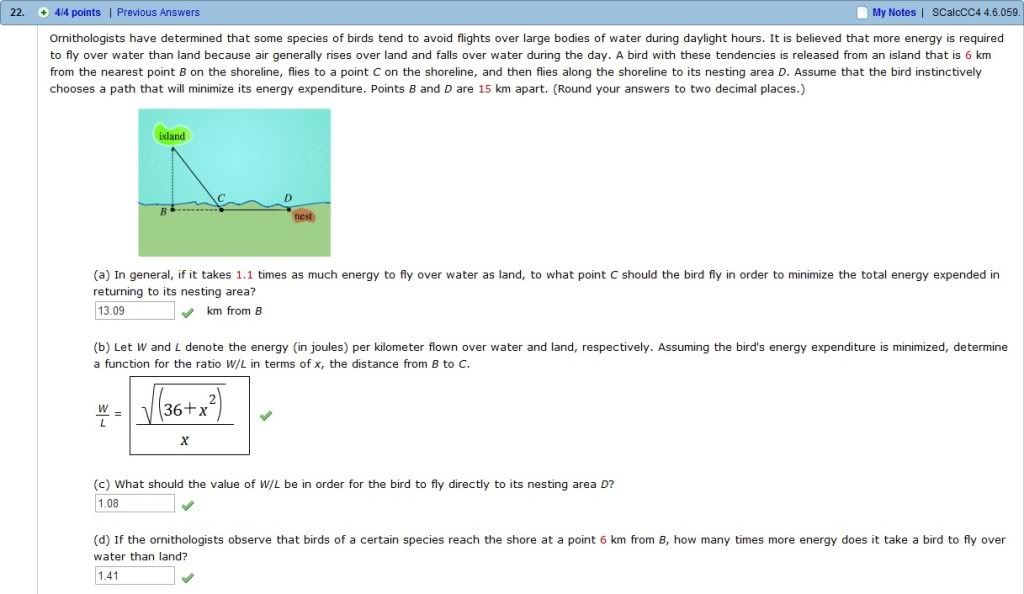
题目在这里,我对这道题的第三问感到一些疑惑……
我觉得:在水路飞行消耗能量W和陆路飞行消耗能量L一致,也就是W/L = 1的时候,就无所谓陆路或者水路,最节省能量的飞行方式是从岛直接飞往巢穴(D)点,因为两点间线段最短。
但是得出的答案却不是这样。
第三题答案显示当W/L = 1.08(此处我近似到小数点后两位)时直接水路飞往D点可以最小化消耗能量。
……请问为什么会这样呢-。-|
我自己也重新找了这道题的类似题(就是改动了数据,将岛到对岸的直线距离改为4km,|BD|改为16km),得出的结果是当W/L = 1.03时直接飞往D点最节省能量。
一般说来水路飞行和陆路飞行消耗的能量对于同一只鸟来说都是固定的,为什么这个比值还会和|BD|有关呢?
……想不通……
求指导……
//////////////////////////////////////////
我又看了一下,对于第二问得出的分式而言,W/L的值还不能为1……
……为啥会这样呢= =|
能量消耗效率怎么会随距离变化而变化呢……
的确,可以通过距离求出效率,但是得出的结论应该是比值是无关距离的一个量才对啊-。-|
}